大话西游2数据大神烧脑风暴 上限抽剖析与装备搭配

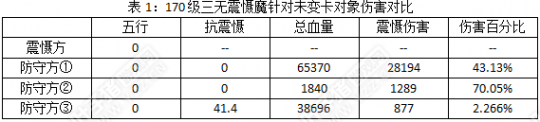
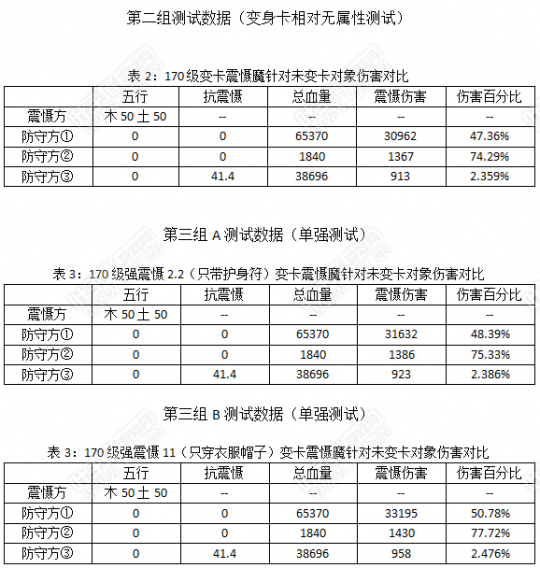
　　最近，“上限抽”普遍进入大家的视野，其实有很多玩家都不懂它的意思，甚至很多人只懂得四级+忽视F就是上限，连为什么都不懂，笔者也烦躁了很久，索性去研究了下，也发现了计算器上的一些小漏洞，特此呈现如下。

    >>推荐阅读:叶子猪故事会第一期 他生于煤矿死于煤矿

　　本文共分三章，数据量庞大，难受的读者可以直接观看结论。

　　第一章 魔震慑公式的推导过程

　　震慑方基本数据：170级女魔，熟练度25176，天赋未满20点无任何强化属性

震慑方

　　防守方①：178级女魔，三世男魔转，无任何震慑抗性

防守方1

　　防守方②：未转31级女仙，无任何震慑抗性

防守方2

　　防守方③：172级男仙，三世女魔转，抗震慑41.4%

防守方3

　　第一组测试数据

第一组测试数据

　　大话精灵给予的回答震慑血量上限50%，显示法术震慑血量的值为42%，当然我们可以假设在42.00%~42.99%的范围内结果都是合理的，因为大话2的数据通常只显示整数位，小数点后的N位数不会显示，但也不会四舍五入。

　　按理说，无影响的公式应该为实际伤害=法术震慑血量×HP

　　这是实验最纯粹的为0假设，在没有任何外力影响下，但是很明显都不符合①②。说明这个公式不完整。问题有以下几点。

　　问题1：震慑法术的描述吸取对方血量42%:和①的百分比结果不符合，不在合理范围内

　　问题2：震慑血量的上限50%与②的百分比结果不符合，大大超出这个上限值

　　问题3：为什么①和②均无抗震慑伤害百分比却不一致

　　问题4：为什么有些小怪一抽即死(长安东、境内、吉人天相触发后)

　　推论1：系统描述不会有错误，可能只是概念相对模糊。这个结果其实和系统说的50%并不相悖，似乎只有没完全说清楚的嫌疑。那我们有理由设想，存在一个额外的伤害导致伤害百分比变化，而且这个伤害不在震慑范围内，不然无法解释①与②的结果。因为参数不足，无法得知这些数据是否达到上限，所以进行第二组、第三组测试，当伤害已经无法再附加那么说明已达到血量伤害上限。

 

 测试数据表

　　测试到这里的时候，关乎无属性伤害测试数据基本就完善了。

　　对比第三组B和第五组，①和②在数据加强的时候伤害却已经没有了变化，说明真的存在上限伤害，并且已经达到了上限值，再一次说明推论1的正确性，肯定存在一个额外伤害，使总伤害上限超过50%，按照50%计算震慑上限(并不是总伤害上限)，则有额外的伤害

　　①=0.78%×65370=510，

　　②=27.72%×1840=510，

　　这两个额外伤害是恒定的，刚好是震慑方等级的3倍，当然这里暂时是猜想。

　　后来又进行了166级女魔的上限震慑实验(这里不再列出，因数据量庞大)，得到的结果是498点，也恰好额外伤害是等级的3倍，那么我们有理由相信，这个额外伤害已经确定为一个常量，也就是+等级×3，因与等级有关，我们可以叫等级伤害。既然是额外伤害，那么联结前面的内容，必然是相加的伤害并且与50%无关，所以得公式

　　实际伤害=法术震慑血量×HP+等级×3

　　这个数值确定后，可以完美解释问题中的所有无法回答的内容，接着回头反推第一组数据.

　　此时为了精确数值，毕竟法术震慑血量在该熟练度下肯定是个定值，而因大话2无四舍五入的原因，因此必须让第一组数据带上小数点后从00~99推测各种可能性，可以取最小分母/最大分子~最大分母/最小分子之间的数值，也叫范围确定法。

　　代入①，法术震慑血量介于(28194.00-510)/65370.99~(28194.99-510)/65370.00，得出震慑血量常量介于42.349%~42.351之间，

　　代入②，答案介于(1289.00-510)/1840.99~(1289.99-510)/1840.00之间，得42.314%~42.391%之间，

　　因两个都是无差异的正确答案范围，因此取公共部分，得42.349%~42.351%之间，假若取更多不同血量的实验体，那么很显然会接近这两者的平均数，也就是42.35%，所以法术震慑血量中所显示的42%的实际值就是42.35%了，那么公式进一步升级

　　实际伤害=42.35%×HP+等级×3

　　紧接着可以推断第二组数据了，变卡的影响看上去伤害均已升值，按照仙族变卡伤害1.1倍的描述，我们可以假设魔族变卡后也会是个定值的倍数伤害，那么这个定值应该在公式的哪个地方加进去呢，有三种方案

　　1、加成在HP项部分，那么有：

　　实际伤害=42.35%×HP×变卡伤害倍数+等级×3

　　①得变卡伤害倍数=1.0999778，

　　②得变卡伤害倍数=1.0997895

　　因两者十分接近，非常有可能就是正确答案，此时若有小数点位影响答案≈1.1

　　2、加成在等级伤害部分，那么有：

　　实际伤害=42.35%×HP+等级×3×变卡伤害倍数

　　①得变卡伤害倍数=6.4271，

　　②得变卡伤害倍数=1.1525

　　两者差距很远，说明此方案可排除

　　3、加成在整体部分，那么有：

　　实际伤害=(42.35%×HP+等级×3)×变卡伤害倍数

　　①得变卡伤害倍数=1，

　　②得变卡伤害倍数=1

　　两者虽一样，但是很明显数据显示伤害已经有加成，而不是1倍伤害，说明此方案也可排除

　　因为方案1正确，得到进一步的公式

　　实际伤害=42.35%×1.1×HP+等级×3

　　然后我们可以对比第二组和第三组A的测试数据，为什么不取第三组B的数据呢，因为第三组B的数据①②已经达到上限，也就是极有可能已经超过系统界定的50%，所以会产生很多误差，所以只能取A组未满伤害研究关系。

　　此时只是多了强震慑2.2%，强震慑该加在哪个地方，同理于如上的三个方案，分别得

　　方案1，①1.022②1.022，留待观察

　　方案2，①2.313②1.307差距大，排除

　　方案3，①②都是1，伤害又没变化，可排除。

　　看上去方案1唯一和2.2%搭边的就是和1有相加关系，即(1+2.2%)=1.022，那么只有这样的可能

　　实际伤害=42.35%×1.1×(1+强%)×HP+等级×3

　　接着，就是研究忽视的关系，取第二组和第四组的测试数据，忽视1.4%的加成模式参照3个方案，分别得

　　方案1，①1.033②1.03247，留待观察

　　方案2，①2.9733②1.0546，差距大，可排除

　　方案3，①②都是1，伤害又没变化，可排除

　　到这里，方案1的加成位置基本可以判定是对的，但是无法找出这1.4%的关系，换个思路讲，也有可能和42.35%×1.1×HP中的一项找出联结，那很明显就只能和42.35%有关系了。

　　这个42.35%和1.4%该怎么样形成关系，会得到方案1的结果①1.033倍伤害②1.03247倍伤害，那么存在几种形式有

　　1、42.35%+忽

　　2、42.35%-忽

　　3、42.35%×忽

　　4、42.35%÷忽

　　5、42.35%×(1+忽)

　　6、42.35%÷(1-忽)

　　很明显，2、3、4已经偏离1.033左右的倍数，不符合，那么可以将其代入，

　　最后得出

　　1答案=(42.35%+忽)/42.35%=1.033

　　5答案=1+忽=1.014，不符合

　　6答案=1/(1-忽)=1.0142，不符合

　　所以1形式成立

　　因此公式扩充为

　　实际伤害=(42.35%+忽%)×1.1×(1+强%)×HP+等级×3

　　推论到了这一步，迟迟未上场的防守方③可以上次了，就是抗震慑的影响，采取和忽视与全公式影响的各种可能性，最后可得出趋于完整的公式(同上推论过程，较繁琐，不再列出)

　　实际伤害=(42.35%+忽-抗)×1.1×(1+强%)×HP+等级×3

　　只差最后一项属性，也就是对无属性伤害%的影响，同理于前面单强的推论，综合50%上限的判定，最后得出五法震慑熟练25176对无属性对象伤害的完全公式：

　　实际伤害=(42.35%+忽%-抗%)×(1+强%)×(1+无属性%)×1.1×HP+等级×3

　　其中红色部分总积≤50%，若>50%则按50%计算。

　　当实际伤害≤1时，实际伤害最终=1;

　　克抽魔的伤害公式推论要比对无属性抽魔的计算要复杂，直接略过，最后得

　　实际伤害=(42.35%+忽%-抗%)×(1+强%)×【(1+克金%×木%)×…×(1+克火%×金%)】×【1+(金×木+…+火×金—木×金—…—金×火)×0.4】×HP+等级×3

　　其中红色部分总积≤50%，若>50%则按50%计算。

　　当实际伤害≤1时，实际伤害最终=1;

　　当你变的卡是某五行100并且将无属性NPC提克，可以将上述公式简化，如土克水，被提克后水50，得

　　实际伤害=(42.35%+忽—抗)×(1+强%)×(1+克水%×水50%)×(1+土100%×水50%×0.4)×HP+等级×3

　　其实先从公式的相似性上比较， 4级神兵魔都没什么了不起，只不过克水抽也有难处，除非能混到吻合的队伍。神兵除了比16级满值强7.2多2.8的震慑，但却在属性伤害上输给克水抽，1.1倍<1.2倍。退一万步讲，都假设这个效果相等，那么要求 (1+无属性40%)≤(1+克水%×水50%)，只需克水80点以上足矣，这对一个克魔不是很难。